Appendix A — Life Tables, Markov Chain and APIs

A.1 Life Tables and Life Expectancy

Back in the 1700s the Swiss mathematician and physicist Daniel Bernoulli (1700 - 1782) developed the use of a life table model by differentiating life tables based on specific causes of death.¹

Originally made by the English scientist John Graunt (1620-1674), for the analysis of the mortality of the population of London and the impact of different diseases. Life tables contain fundamental statistics for the calculation of probabilities of deaths and the computation of life expectancy at birth and at different ages.

A.1.1 Life tables components

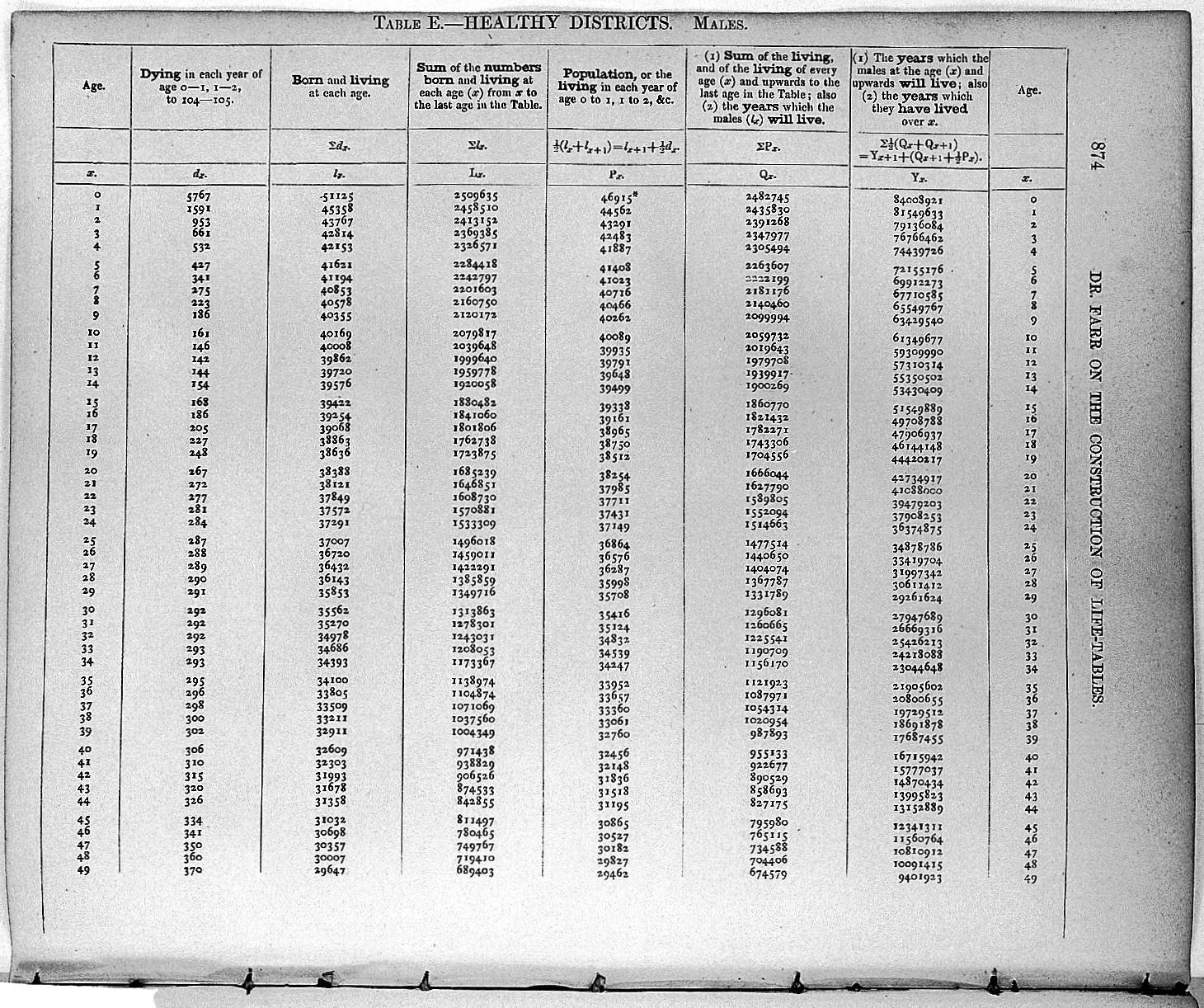
More recent life tables are standardized to be used for a population of 100 000 at age 0.

l_x survivors at age x it starts with a value of 100 000

d_x deceased at age x

q_x probability of deaths

p_x probability of survival

The probability of survival is given by: p_x=1-q_x

Let’s start constructing a life table

The Global Life Tables are included in the hmsidwR package as gho_lifetables dataset. This dataset has been released by the WHO, and contains various indicators.

The construction of the Global Life Tables takes consideration of age-specific mortality patterns, which is the main improvements made on life tables construction since the first set of model life tables published by the United Nations in 1955, see² for more information about a detailed procedure.

To have a look at the package documentation for this dataset, use:

?hmsidwR::gho_lifetables

library(tidyverse)
hmsidwR::gho_lifetables %>%
  count(indicator) %>%
  select(-n)
#> # A tibble: 7 × 1
#>   indicator
#>   <chr>    
#> 1 Tx       
#> 2 ex       
#> 3 lx       
#> 4 nLx      
#> 5 nMx      
#> 6 ndx      
#> 7 nqx

The indicator of interest for re-building a life table are:

lx - number of people left alive at age x
age

These two key elements are crucial for building the life tables.

lx <- hmsidwR::gho_lifetables %>%
  distinct() %>%
  filter(
    indicator == "lx",
    year == "2019"
  )

x <- lx %>%
  filter(sex == "female") %>%
  select(x = age)

lx_f <- lx %>%
  filter(sex == "female") %>%
  select(lx = value)

lx_m <- lx %>%
  filter(sex == "male") %>%
  select(lx = value)

The probability of survival is calculated as follow:

p_x = \frac{l_x}{l_{x+1}}

px <- lx_f$lx / lag(lx_f$lx)

data.frame(
  x,
  lx = round(lx_f),
  dx = round(c(-diff(lx_f$lx), 0)),
  px,
  qx = 1 - lead(px),
  Lx = c(
    (lx_f$lx[1] + (lx_f$lx[2])) / 2,
    5 * (lx_f$lx[-1] + lead(lx_f$lx[-1])) / 2
  )
) %>%
  head()
#>       x     lx   dx        px          qx        Lx
#> 1    <1 100000 2584        NA 0.025843406  98707.83
#> 2 01-04  97416  915 0.9741566 0.009393050 484790.72
#> 3 05-09  96501  366 0.9906069 0.003790526 481588.68
#> 4 10-14  96135  249 0.9962095 0.002588600 480052.07
#> 5 15-19  95886  305 0.9974114 0.003185671 478666.28
#> 6 20-24  95581  399 0.9968143 0.004179281 476903.98

hmsidwR::gho_lifetables %>%
  distinct() %>%
  mutate(indicator = gsub(" .*", "", indicator)) %>%
  filter(
    indicator == "nLx",
    year == "2019",
    sex == "female"
  ) %>%
  head()
#> # A tibble: 6 × 5
#>   indicator  year age   sex      value
#>   <chr>     <dbl> <ord> <chr>    <dbl>
#> 1 nLx        2019 <1    female  97857.
#> 2 nLx        2019 01-04 female 387467.
#> 3 nLx        2019 05-09 female 481589.
#> 4 nLx        2019 10-14 female 480052.
#> 5 nLx        2019 15-19 female 478666.
#> 6 nLx        2019 20-24 female 476904.

A.1.2 Life expectancy

Life expectancy is the expected number of years a person will live, based on current age and prevailing mortality rates. There are several methods to calculate life expectancy, but one common approach is to use the actuarial life table, which is a statistical table that provides the mortality rates for a population at different ages. The following steps can be used to calculate life expectancy using a life table:

Identify the relevant mortality rates for the population and time period of interest. Calculate the probability of surviving to each age, given the mortality rates. Multiply the probability of surviving to each age by the remaining life expectancy at that age to obtain the expected number of years of life remaining at each age. Sum the expected number of years of life remaining at each age to obtain the total life expectancy. Note that life expectancy is a statistical estimate and can be influenced by many factors, such as lifestyle, health, and environmental factors, so actual individual life expectancy can vary widely.

Here are some key references for calculating life expectancy:

United Nations World Population Prospects - The UN provides detailed life tables and population data, including life expectancy, for countries and regions around the world.
Centers for Disease Control and Prevention (CDC) - The CDC provides life tables for the United States, as well as information on how life expectancy is calculated and factors that affect it.
World Health Organization (WHO) - The WHO provides information on global health and life expectancy, including data and reports on trends in life expectancy and mortality.
Actuarial Science textbooks - Books such as “Actuarial Mathematics” by Bowers, Gerber, Hickman, Jones, and Nesbitt, or “An Introduction to Actuarial Mathematics” by Michel Millar, provide comprehensive coverage of the methods and mathematics used in calculating life expectancy.
Journal articles - Articles in actuarial and demographic journals, such as the North American Actuarial Journal or Demographic Research, often provide in-depth coverage of the latest research and methods for calculating life expectancy.

A.2 Markov Chain

A Markov chain is a stochastic model describing a sequence of possible events in which the probability of each event depends only on the state attained in the previous event. The state space of a Markov chain is the set of all possible states of the system. The transition probabilities are the probabilities of moving from one state to another. The transition matrix is a square matrix that describes the transition probabilities between states.

The code for this replication of the Markov Chain is from Dobrow - Bayesian analysis of infectious diseases book (chapter4). It shows clearly how to create a Markov chain and calculate the transition probabilities.

set.seed(000)
markov <- function(init, mat, n, labels) {
  if (missing(labels)) labels <- 1:length(init)
  simlist <- numeric(n + 1)
  states <- 1:length(init)
  simlist[1] <- sample(states, 1, prob = init)

  for (i in 2:(n + 1)) {
    simlist[i] <- sample(states, 1, prob = mat[simlist[i - 1], ])
  }

  labels[simlist]
}

P <- matrix(c(.51, .49, .49, .51),
  nrow = 2, ncol = 2, byrow = TRUE
)
init <- c(1, 0)

markov(init = init, mat = P, n = 100)
#>   [1] 1 1 1 2 1 1 2 1 2 1 1 1 1 2 2 1 1 2 1 1 2 1 1 2 2 2 2 2 2 1 1 1 2 2 2 1 2
#>  [38] 1 1 2 2 1 2 1 2 1 2 2 2 1 2 2 1 1 1 1 1 1 2 1 1 2 2 2 2 1 1 1 2 2 1 1 2 2
#>  [75] 2 2 1 2 2 1 2 2 1 1 1 2 2 1 1 1 1 1 1 2 1 2 1 1 1 2 1

# Define the number of transitions
n_transitions <- 10000

# Simulate Markov chain
simulated_chain <- markov(init, P, n_transitions)

# Calculate the transition probabilities
transition_counts <- table(
  simulated_chain[-1],
  simulated_chain[-(n_transitions + 1)]
)
transition_probabilities <- transition_counts / rowSums(transition_counts)
transition_probabilities
#>    
#>             1         2
#>   1 0.5140224 0.4859776
#>   2 0.4844249 0.5155751

# Calculate prior probabilities
prior_probabilities <- table(simulated_chain[-n_transitions]) / n_transitions

# Calculate posterior probabilities
posterior_probabilities <- transition_probabilities %*% prior_probabilities

# Print prior probabilities
print("Prior probabilities:")
#> [1] "Prior probabilities:"
print(prior_probabilities)
#> 
#>      1      2 
#> 0.4992 0.5008

# Print posterior probabilities
print("Posterior probabilities:")
#> [1] "Posterior probabilities:"
print(posterior_probabilities)
#>    
#>          [,1]
#>   1 0.4999776
#>   2 0.5000249

A.3 Collecting Data with APIs

Collecting data to use in a research analysis involves a selection of sources and methods to use for optimizing computational time when downloading and reading the files. Once data is set and ready to use a further step is required to make the data suitable for the selected model. The source of data is an important variable. Generally, data can be downloaded by using an API (application programming interface) which allow the user to get access to data directly from source, with the use of specified back-end computations. There are alternatives at using an API; data can be obtained by downloading it directly into the computer,or loaded through library packages. Usually, available files are provided under various forms such as delimited type of files, .csv, .xls, .json, and other types. Here is an example of how to use an API for downloading a file directly onto your computer.

library(httr)
url <- ""
httr::GET(url = url)

A.3.1 Download Data with APIs

A.3.1.1 IHME Data APIs

Head over https://ghdx.healthdata.org/ihme-api to get access to the IHME API’s page. The page provides IHME APIs for Sustainable Development Goals (SDG) data. Then, click on https://api.healthdata.org/sdg to login and request an API key. More information on the methodology and data can be found at https://www.gatesfoundation.org/goalkeepers/report/2024-report/data-sources/#ExploretheData.

Load necessary libraries:

library(httr)
library(jsonlite)
library(tidyverse)

The IHME API provides the following queries. These queries might be updated in the future, so it is important to check the API documentation for the most recent queries.

SDG Query Input:
- GetGoal
- GetIndicator
- GetTarget
- GetLocation
- GetAgeGroup
- GetScenario
- GetSex
- GetResultsByTarget
Query Input for Results:
- GetResultsByTarget
- GetResultsByIndicator
- GetResultsByLocation
- GetResultsByYear

Use the function gbd_get_data to download data from the IHME API. The function requires the following arguments in quotation marks:

The url where to download the data, such as: "https://api.healthdata.org/sdg/v1"
An API key = “YOUR-KEY”
A sdg-endpoint, such as: “GetResultsByLocation?location_id=86&indicator_id=1002&year=2019”

The function returns a data frame with the results.

gbd_get_data <- function(url, key, sdg) {
  library(httr)
  library(jsonlite)
  url <- paste0(url, "/", sdg)
  headers <- c("Authorization" = key)
  res <- GET(url, add_headers(headers))
  data <- fromJSON(rawToChar(res$content))
  data <- data$results
}

Build the query to download results by adding specification of the data. Let’s start with:

GetIndicator

indicator <- gbd_get_data(
  url = "https://api.healthdata.org/sdg/v1",
  key = "YOUR-KEY",
  sdg = "GetIndicator"
)

As an example, let’s see the first 6 indicators.

library(tidyverse)
indicator %>% 
  select(indicator_id, indicator_name) %>% 
  arrange(indicator_id) %>%
  head()

Then use the indicator_id to download the data for a specific indicator.

agegroup <- gbd_get_data(
  url = "https://api.healthdata.org/sdg/v1",
  key = "YOUR-KEY",
  sdg = "GetAgeGroup"
)
agegroup %>%
  select(age_group_id, age_group_name) %>% 
  arrange(age_group_id) %>%
  head()

dat19 <- gbd_get_data(
  url = "https://api.healthdata.org/sdg/v1",
  key = "YOUR-KEY",
  sdg = "GetResultsByIndicator?indicator_id=1001&location_id=86&year=2019"
)

dat19%>%
  select(location_name, indicator_name, sex_label, mean_estimate)

Figure A.4: GBD-SDG Tuberculosis Data 2019

The same data can be downloaded using the httr package. The following code downloads the data for the indicator with indicator_id = 1001, location_id = 86, and year = 2019.

headers <- c("Authorization" = "YOUR-KEY")
res <- GET(url="https://api.healthdata.org/sdg/v1/GetResultsByIndicator?indicator_id=1001&location_id=86&year=2019",
           add_headers(headers))

res$content%>%
  rawToChar() %>%
  fromJSON()

An advanced version of the gbd_get_data() function can be found in the hmsidwR package. The function hmsidwR::gbd_get_data() allows the user to endpoint customisation, instead of using sdg argument with the long query string, an endpoint is used to specify the starting point of the quesry, such as GetResultsByIndicator. Then, the user can specify the indicator_id, location_id, and year to download the data for specific indicator, location, and year.

The function requires the arguments to be within quotation marks:

hmsidwR::gbd_get_data(
  url = "https://api.healthdata.org/sdg/v1",
  key = "YOUR-KEY",
  endpoint = "GetResultsByIndicator",
  indicator_id = "1001",
  location_id = "86",
  year = "2019"
)

The output is still the same as Figure A.4 in the previous example.

A.3.2 Package References

The {hmsidwR} package is available at https://github.com/Fgazzelloni/hmsidwR. The package provides data and functions to support this book.

Download the package from CRAN or for the development version use GitHub:

# Download from CRAN
install.packages("hmsidwR")

# Download from GitHub
# install.packages("devtools")
devtools::install_github("Fgazzelloni/hmsidwR")

“Life Table - an Overview | ScienceDirect Topics,” n.d., https://www.sciencedirect.com/topics/medicine-and-dentistry/life-table.↩︎
“Modified Logit Life Table System: Principles, Empirical Validation, and Application: Population Studies: Vol 57, No 2,” n.d., https://www.tandfonline.com/doi/abs/10.1080/0032472032000097083.↩︎